Electric field on equatorial line of electric dipole

 2.  For points on the equatorial plane : 

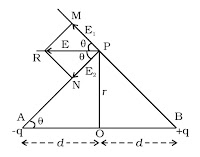
Consider an electric dipole AB. Let 2d be the dipole distance and p be the dipole moment. P is a point on the equatorial line at a distance r from the midpoint O of the dipole (Fig.).

         

Fig. Electric field at a point on equatorial line & Components

Electric field at a point P due to the charge +q of the dipole,

E1= q / [4πεo (BP^2) ]   (along BP) 

E1= q / [4πεo (r^2+d^2) ]   (along BP)     (∵BP^2 = OP^2 + OB^2)

                                                                              

Electric field (E2) at a point P due to the charge –q of the dipole

E2 = q / [4πεo (AP^2) ]   (along PA)

E2 = q / [4πεo (r^2+d^2) ]   (along PA)

The magnitudes of E1 and E2 are equal. Resolving E1 and E2 into their horizontal and vertical components (Fig.), the vertical components E1 sin θ and E2 sin θ are equal and opposite, therefore they cancel each other.

The horizontal components E1 cos θ and E2 cos θ will get added along PR.

Resultant electric field at the point P due to the dipole is

  

E = E1 cos θ + E2 cos θ  (along PR)

E = 2 E1cos θ      ( ∵  E1 = E2 )

E = q / [4πεo (r^2+d^2)]  x 2 cos θ

but cos θ = d / (r^2+d^2)^1/2

E = q / [4πεo (r^2+d^2)] x 2 d / (r^2+d^2)^1/2

E = p / [4πεo (r^2+d^2)^3/2]        (∵p = q2d)

                  

For a dipole, d is very small when compared to r

E = p / [4πεo r^3]

The direction of E is along PR, parallel to the axis of the dipole and directed opposite to the direction of dipole moment.