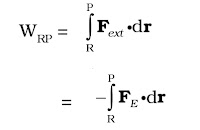Consider an electrostatic field E due to some charge configuration. First, for simplicity, consider the field E due to a charge Q placed at the origin. Now, imagine that we bring a test charge q from a point R to a point P against the repulsive force on it due to the charge Q. With reference to Fig., this will happen if Q and q are both positive or both negative. Let us take Q, q > 0.
Fig. A test charge q (> 0) is moved from the point R to the point P against the repulsive force on it by the charge Q (> 0) placed at the origin.
We assume that the test charge q is so small that it does not disturb the original configuration, namely the charge Q at the origin (or else, we keep Q fixed at the origin by some unspecified force), in bringing the charge q from R to P, we apply an external force F(ext) just enough to counter the repulsive electric force F(E) (i.e, F(ext)= –F(E)).
This means there is no net force on or acceleration of the charge q when it is brought from R to P, i.e., it is brought with infinitesimally slow constant speed. In this situation, work done by the external force is the negative of the work done by the electric force, and gets fully stored in the form of potential energy of the charge q.
If the external force is removed on reaching P, the electric force will take the charge away from Q – the stored energy (potential energy) at P is used to provide kinetic energy to the charge q in such away that the sum of the kinetic and potential energies is conserved.
Thus, work done by external forces in moving a charge q from R to P is
Let us assume electrostatic potential energy zero at infinity, if we take the point R at infinity, we get,
W (∞P) = U(P)−U(∞)
Since the point P is arbitrary, provides us with a definition of potential energy of a charge q at any point.
Potential energy of charge q at a point is the work done by the external force (equal and opposite to the electric force) in bringing the charge q from infinity to that point.